Riscaldati per il cervello: puoi risolvere il problema delle monete contraffatte? Controlla!

Il matematico ha solo tre tentativi, quindi non puoi pesare ogni moneta separatamente. Devi dividerli in pile e metterli sulla bilancia più pezzi alla volta, avvicinandoti gradualmente a quello falso.

Supponiamo che un matematico abbia deciso di dividere 12 monete in tre pile di quattro monete ciascuna. Quindi ha messo quattro monete su ciascuna scala. Questa pesatura può dare due risultati. Consideriamo ciascuno di loro.

1. Il peso delle due pile di monete era lo stesso. Pertanto, tutto il denaro in esse contenuto è reale e la contraffazione si trova da qualche parte tra le quattro monete non ponderate.

Per tenere traccia del risultato, il matematico contrassegna tutti gli script con uno zero. Quindi ne prende tre e le confronta con tre monete non pesate. Se il loro peso è uguale, la moneta non ponderata rimanente (quarta) è contraffatta. Se il peso è diverso, il matematico mette un più sulle tre monete non contrassegnate se sono più pesanti di quelle con zero, o un meno se sono più leggere.

Poi ne prende due monetecontrassegnato con più o meno e confronta il loro peso. Se è lo stesso, la copia rimanente è falsa. In caso contrario, il matematico guarda i segni: tra le monete con un più, il falso sarà quello più pesante, tra le monete con un meno, quello più leggero.

2. Il peso delle due pile di monete non era lo stesso.

In questo caso, il matematico deve agire in questo modo: segnare i soldi in una pila pesante con un più, in una pila leggera con un meno, in una pila non ponderata con uno zero, poiché è noto che la copia falsa era sulla bilancia.

Ora devi raggruppare le monete per mantenerle entro le due pesate rimanenti. Uno dei modi è prendere invece di tre monete con un più, tre monete con un meno e mettere tre pezzi con uno zero al loro posto.

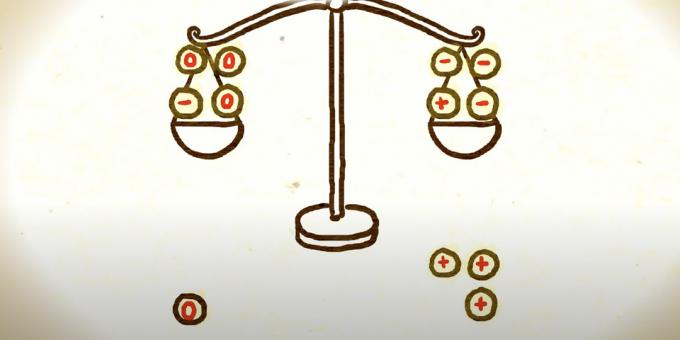
Seguono tre possibili opzioni. Se quella scala che era più pesante supera ancora, allora o la vecchia moneta con il segno più è più pesante delle altre, oppure la moneta con il segno meno sull'altro lato della bilancia è più leggera. Un matematico deve sceglierne uno e confrontarlo con uno schema comune per trovare un falso.

Se il piatto di pesata, che era più pesante, è diventato più leggero, allora una delle tre monete con un segno meno mosse dal matematico è la più leggera. Ora ha bisogno di confrontarne due sulla bilancia. Se i risultati sono pari, la terza moneta sarà contraffatta. Con la disuguaglianza, il falso è più facile.

Se, dopo aver cambiato le ciotole, vengono bilanciate, una delle tre monete tolte dalla bilancia con il segno più è più pesante delle altre. Un matematico deve confrontarne due. Se sono uguali, il terzo è falso. In caso di disuguaglianza, il falso è quello più pesante.

L'imperatore annuisce con approvazione mentre ascolta il ragionamento matematica, ma il governatore disonesto va in prigione.

Questo puzzle è la traduzione di un video TED-Ed.